Tag: maths

Calculating the Number of Segments for Accurate Circle Rendering

A common way to draw circles with any kind of vector graphics API is by approximating it with a regular polygon, e.g. as a regular polygon with 32 sides. The problem with this approach is that it might look good in one resolution, but crude in another, as the approximation becomes more visible. So how do you pick the right number of sides N for the job? For that, let’s look at the error that this approximation has.

A whole bunch of math

I define the ‘error’ of the approximation as the maximum difference between the ideal circle shape and the approximation. In other words, it’s the difference of the inner radius and the outer radius of the regular polygon. Conveniently, with a step angle \alpha=\frac{2\pi}{N} the inner radius is just the outer radius r multiplied by the cosine of half of that: r\times\cos\frac{\alpha}{2}. So the error is r-r\times\cos\frac{\pi}{N}. I find it convenient to use relative error \epsilon for the following, and set r=1:

\epsilon=1-cos\frac{\pi}{N}

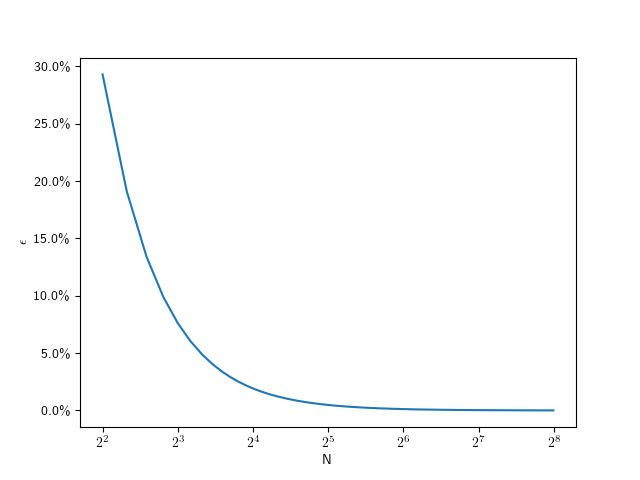
The following plot shows that value for N going from 4 to 256:

Plot showing the relative error numbers of subdivision

As you can see, this looks hyperbolic and the error falls off rather fast with an increasing number of subdivisions. This function lets use figure out the error for a given number of subdivisions, but what we really want is he inverse of that: Which number of subdivisions do we need for the error to be less than a given value. For example, assuming a 1080p screen, and a half-pixel error on a full-size (r=540) circle, that means we should aim for a relative error of 0.1\%. So we can solve the error equation above for N. Since the number of subdivisions should be an integer, we round it up:

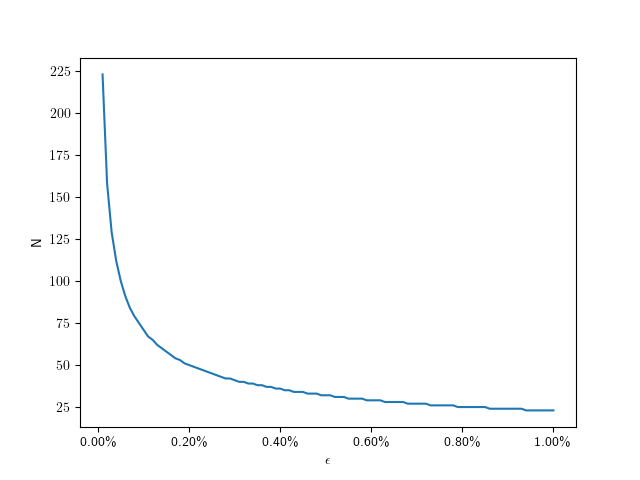
N=\lceil\frac{\pi}{\arccos{(1-\epsilon)}}\rceil

So for 0.1\% we need only 71 divisions. The following plot shows the number of subdivisions for error values from 0.01\% to 1\%:

Here are some specific values:

\epsilonN
0.01%223
0.1%71
0.2%50
0.4%36
0.6%29
0.8%25
1.0%23

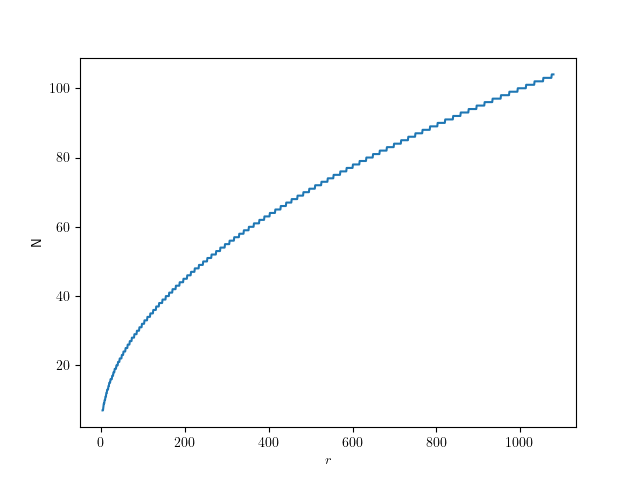
Assuming a fixed half-pixel error, we can plug in \epsilon=\frac{0.5}{radius} to get:

N=\lceil\frac{\pi}{\arccos{(1-\frac{0.5}{radius})}}\rceil

The following graph shows that function for radii up to full-size QHD circles:

Give me code

Here’s the corresponding code in C++, if you just want to figure out the number of segments for a given radius:

std::size_t segments_for(float radius, float pixel_error = 0.5f)
{
  auto d = std::acos(1.f - pixel_error / radius);
  return static_cast<std::size_t>(std::ceil(std::numbers::pi / d));
}